Šodien π (pī) diena56

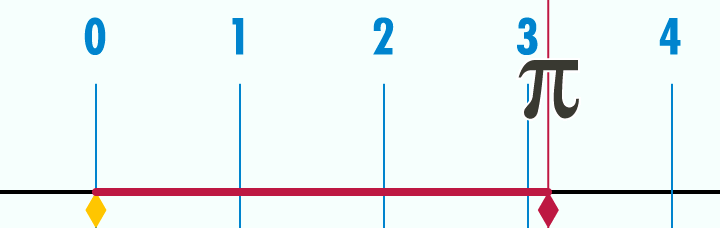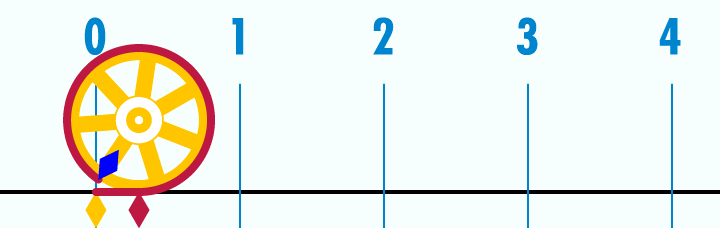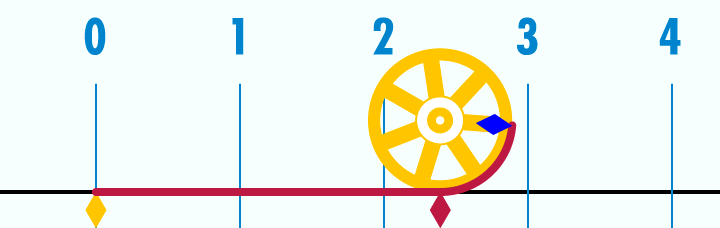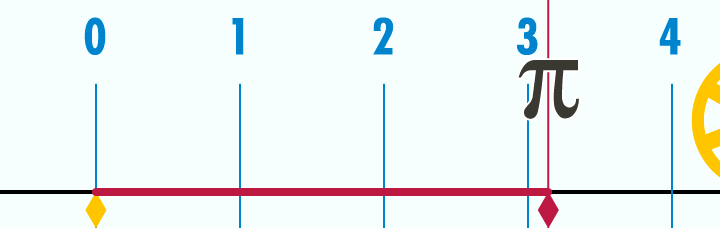
π ir iespējams visatpazīstamākā matemātiskā konstante, kuras aptuvenā vērtība ir 3.14159.....  Pī ir jebkuras riņķa līnijas garuma attiecība pret tās diametru. Tātad, neskatoties uz to, cik liels riņķis tas ir, izdalot garumu ar diametru, rezultāts vienmēr būs π. Tā ir bezgalīga, neperiodiska decimāldaļa. Pī ir iracionāls skaitlis, tātad to nevar uzrakstīt kā attiecību starp diviem veseliem skaitļiem (daļskaitli). Mūsdienu superdatori šim skaitlim jau ir aprēķinājuši 10 biljonus (10^13) ciparu aiz komata. Lai aprēķinātu riņķa, kurš ir redzamā visuma lielumā, apkārtmēru ar precizitāti līdz ūdeņraža atoma izmēram, pietiek tikai ar 38 cipariem aiz komata. Iespējams, ka daudziem pī saistās ar sliktām atmiņām, jo tas tiek plaši izmantots ari trigonometrijā, kuru skolas laikā saprata tikai izredzētie.

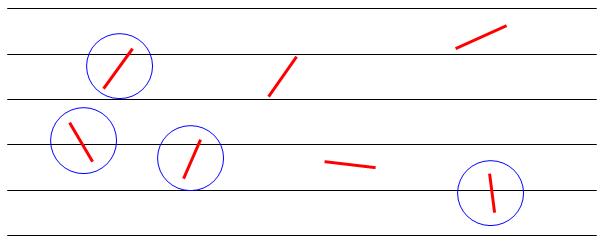
Viens no veidiem, kā mājas apstākļos var aprēķināt aptuveno pī vērtību, ir izmantojot Bufona adatas metodi. Jums būs nepieciešamas vienāda garuma adatas, sērkociņi, vai jebkādi citi štruntiņi, vēlams vairāk kā 100. Uz A3 lapas savelkat paralēlas līnijas, tā, lai atstarpe starp līnijām būtu divreiz lielākā par sērkociņu garumu. Pēc tam "na haļavu" izmētājat sērkociņus pa lapu un izskaitat tos, kuri krusto kādu līniju. Tad izdalat kopējo sērkociņu skaitu ar to sērkociņu skaitu, kuri krustoja līnijas. Rezultātam vajadzētu būt ļoti aptuvenam pī. Jo vairāk sērkociņus izmantosiet, jo precīzāks būs rezultāts.

Nav zināms, vai π ir normāls skaitlis, bet statistikas dati, izanalizējot zinamos pī ciparus, liecina, ka tā ir. Tas nozīmē, ka ka katrs cipars no 0 līdz 9 šajā skaitlī atkārtojas aptuveni vienādu reižu skaitu, proti, ~10% no visiem cipariem ir 1, ~10% divnieku utt. Pī ir bezgalīgi garš, neperiodisks skaitlis, līdz ar to, valda uzskats, ka pī satur jebkuru skaitļu kombināciju, kura nav bezgalīga. Tiesa gan, tas nav pierādīts, bet ja tā ir taisnība, tad kaut kur iekš π var atrast visas pareizās atbildes uz visiem taviem matemātikas kontroldarbiem. Tā kā mums ir zināmi vien 10 biljoni ciparu aiz komata, piedāvāju atrast kaut ko vienkāršāku, piemēram, savu telefona numuru. Domāju, ka lielākā daļa to atradīs, kaut gan šī mājaslapa piedāvā tikai 2 miljardus ciparu. http://www.subidiom.com/pi/