Pilnlauku matemātika ir loģikas nozare, kurā tiek manipulēts ar lauku pārpalikumiem vai matemātiskas darbību attiecināšana uz laukiem, kuri var būt bezgalīgi aizpildīti. Svarīgākais nosacījums pilnlauku matemātikā ir pieņemt sistēmas lauku uz kuru var attiecināt reizināšanu un dalīšanu, tādējādi dodot iespēju tikt pie lauku šķēlumiem vai, reizinot kādu šķeltu lauku, tikt pie pilna lauka.
Pilnlauku matemātikā var izdalīt trīs pamatlauku veidus:
A - sistēmas lauks
B - pilns lauks
C - šķelts lauks
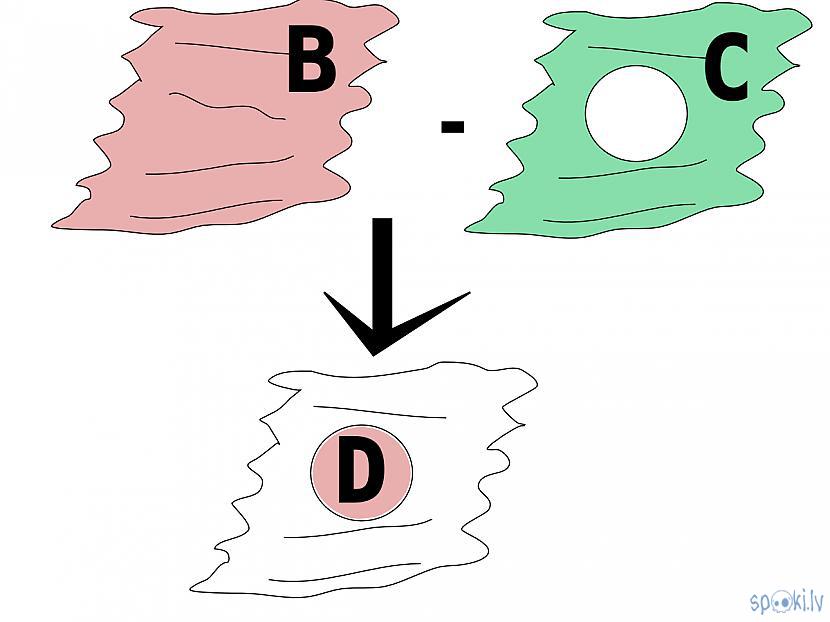
Kā arī palīgluku, kas ir šķelts lauks, tomēr tas ir kā kāda jau esoša šķelta lauka starpība attiecībā pret pilnu lauku:
D - apgriezts lauks
Pilnlauku matemātikas svarīgākais aspekts ir tas, ka attiecinot matemātisku darbību uz sistēmas lauku ir iespējams manipulēt vienlaicīgi ar visiem sistēmas laukā iekļautajiem laukiem, kas pie vajadzības dod iespēju tikt pie vairākiem šķeltiem vai pilniem laukiem vienlaicīgi. Šāda maipulēšana ar laukiem sevi attaisno tad, kad ir nepieciešams iegūt kopēju lauku šķēlumu, kurš nepārklājas vairākos sistēmas laukā iekļautos laukos.
Pilnlauku matemātikas pamatdarbības:
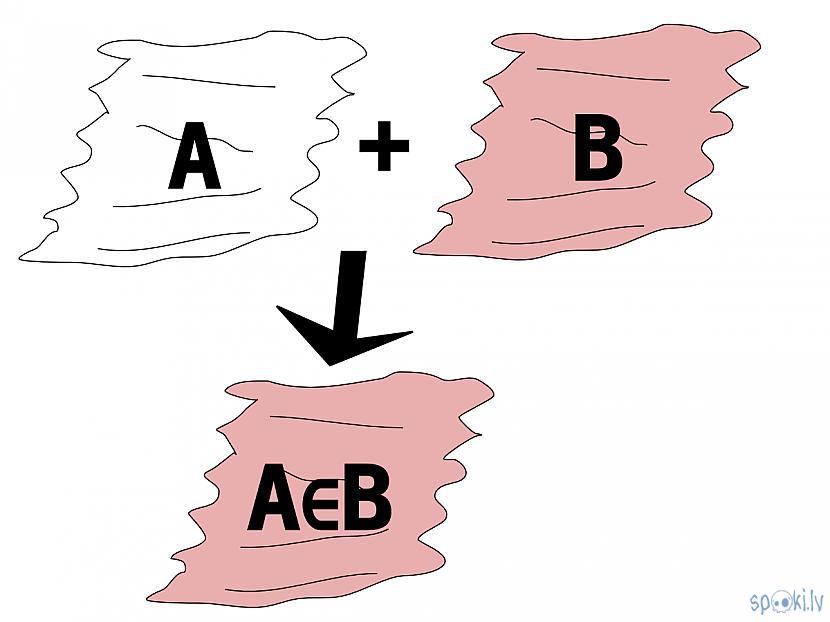
o pieskaitīšana vai iekļaušana
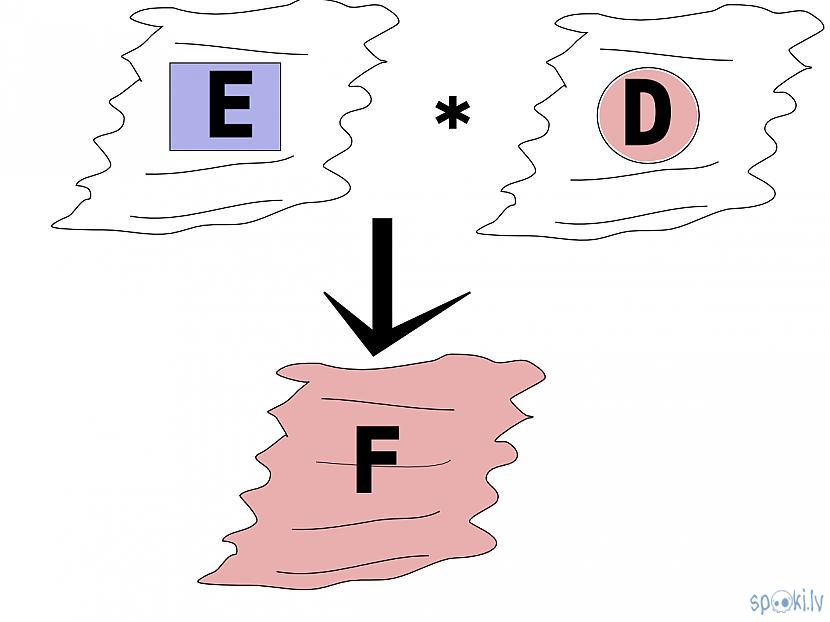
o reizināšana vai lauka pārveidošana par pilnu lauku
o atņemšana vai lauku pārklājumu iegūšana
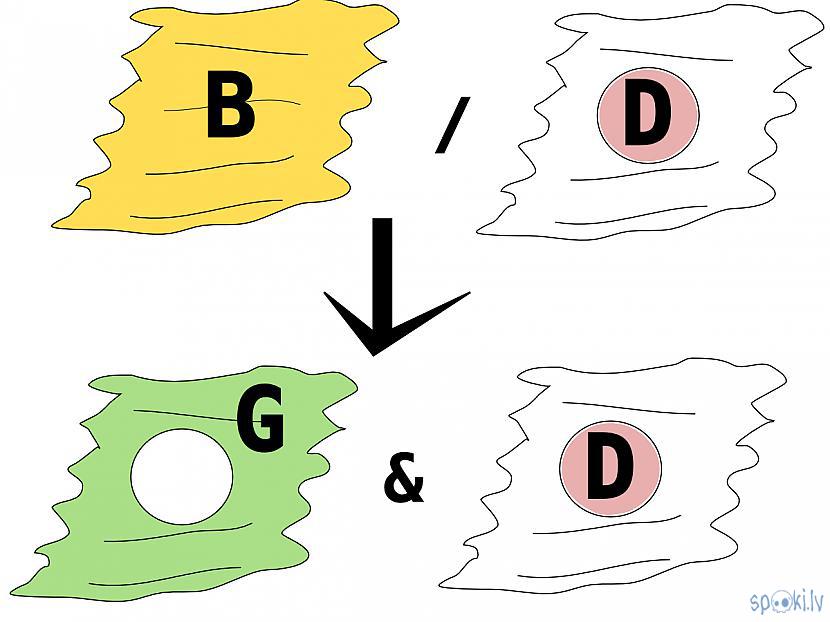
o dalīšana vai apgriezta lauka iegūšana balstoties uz šķeltu lauku, šķeltajam laukam saglabājoties sistēmas laukā pēc darbības veikšanas.
Svarīgākie nosacījumi, kuri ir attiecināmi uz sistēmas lauku:
+ sistēmas lauku reizinot ar kādu citu lauku tiek iegūts pilns lauks
+ sistēmas laukam pieskaitot kādu lauku, tas tiek iekļauts sistēmas laukā
+ tukšu sistēmas lauku dalot ar kādu citu lauku, sistēmas laukā nekas nemainas
+ no sistēmas lauka nevar neko attņemt, pirms sistēmas laukā ir iekļauts cits lauks
Pilnlauku matemātikas pielietojums:
Pilnlauku matemātikas praktiskākā nozīme ir labāka priekštata iegūšana par dažādu virsmu pārklāšanos, kas grafiķiem dod iespēju ātrāk un saprotamāk manipulēt ar dažādām formām plaknē. Pilnlauku matemātika, kā loģikas distance, dod iespēju darboties ar aizpildītas plaknes pārpalikumiem, tā novērtējot lauka aizpildījuma pakāpi.
lasi, vērtē, komentē ![]()