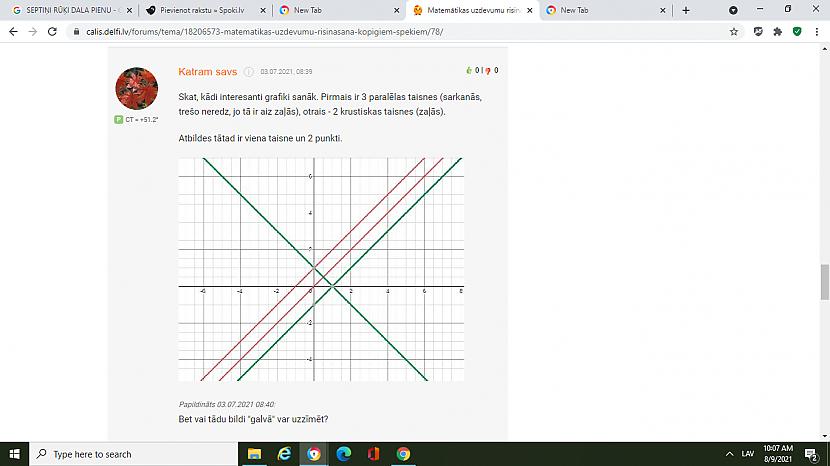
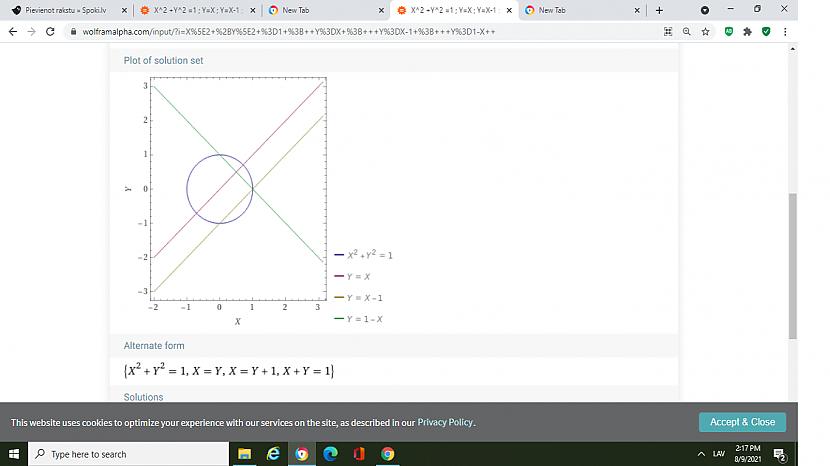
{{{ ( x-y )^3 =x-y ;; (x--1)^2 =y^2 }}}} atrisināt vienādojumu sistēmu
-------------------------------------------------------------------------------------------------------------------------------------------------- HEI SUDENTI !! - studiju un pēījumu cienīgs gadījums -- jauātajums ir par algebras izmanojamības robežām -- skolas algebra pret inženieru matematisko analīzi un geometriju ....... Kadas ir jūsu versijas ??
Vai jūs esie gatavi vadīt kodolreakoru kas būvēts pamaojoties uz vienādojumiem kam bezgalīgi daudz sakņu-- t i vai jūs uztticēttos iekārtai kurai vienalga kādi ir parameri x un y --es personiski ne... es sēsttos pie vadības pults tik tad ja manā ziņā ir dzelžaini nourēt parametrus x no 0 līdz +1 un y no -1 līdz +1 ---- es neesmu pamaskolas sdkolotājs kas māca pliku algebru --zinātni par neko --esmu veterinārs un elekrotehniķis -- ((profesionālis-zinānieks un mākslinieks --3 vienā --- profi informāciju vāc un varbūt arī atceras --zinatnieki infu analizē līdz objektīvi reālā aina izzīmējas--mākslinieki manipulē ar infu lai dizainētu nākotni -- ir vesela rinda gudru profesiju kur vajadzība pēc 3 paralēlāmloģikām --medicīna diplomaija ,karamāksla--- un šis uzdevumiņš vnk ir kĀ radīts lai attlasīu tos kas uz o spējīgi principā --- notestējiet sevi sporta pēc ---man škiet KA TE VAR BŪT VĒL CITĀDI SKAUPUNKTI
Kas ir dots?? 2. un 3 . pakapes polinomu algebriska sistēma vai ļoti konkretu līniju vienādojumi ļotii dzelžaini piejūgti koordinatām ??
Nav srīdu par attbildēm (( x=0,5 y=0,5 )) un (((x=0 y = 1 ))
Domas ļotii dalās --- strīds ir par to vai uz sakrītošām taisnēm y=x-1 ir bezgalīgi daudz sistēmu apmierinošu punktu vai arī tur ir tikai hiperbolas asimptotas fantoms un 2 ļoi konkreti punkti (( x=0 y=-1 )) un (x=1 y=0 )
Infa pārdomām::
Substitūcvija x-y= t dod 1. vienādību fakorizējot t * (t ^2 -1 ) =0 ===>> t = -1 t=0 t=+1 ====> no šejiernes šklietami 3 taisnes y= x+ t kur t pieņem vērības -1 ;0;+1 --- šie cipari t ir sarpības starp derīgiem x un y --- nav gluži tas pas kas punkti uz Y ass jeb LINEĀRO funkciju viendojumos tipa y=ax+b SĀKUMA ORDINĀTAS ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- fakorizējot 1. vienādību pa tiešo iegūst (X-Y) * ( (x-y)^2-1 ))=0
===>> ( x-y) * ( x-y +1 ) * (x-y -1) = 0 ( izskatās pēc 3 taišņu viernadojumie --tikai vieninieku zīmes konfliktē ar t zīmēm )) ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- galu galā ir citi identiski pārveidojumi un to interprettācijas ( X-y )^2 -1 =0 ===> x^2 + y^2 =R^2 = 2xy-1 (( aplis ar centru x=0 y=0 ))
===> x^2/2xy+1 + Y^2/ 2xy +1 = 1 ((elipses vai apļa vienādojums kur cenrs x=0 y=0 be R^2= 2xy+1 ((ievieojot centra koordinās R=1 ) --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- asnalogi 2 vienādība x^2 - 2x +1 -Y^2 =0 ===> x^2-y^2= 2x-1 === x^2/2x-1 -y^2/2x-1 =1
hiperbolas vienĀDOJUMS KUR CENRS X=1 Y=0 --bet imaginārie un reālie radiusi/pusasis pēc x=1 ievieyošanu kļust par 1........................................ tieši to pašu iegūst ja nodala mainīgos hiperbolas vienadojumam
x^2 -2x = y^2-1 ====>> x (x-2) = (y-1)(y+!) ===> līnijas x=0 x=2 y=+1 y=_1 acīmredzami iezīmē reālo un imagināro pusasu taisnstūri ap hiperbolas centtru punkā x=1 y=0